
我喜欢将数学概念转化为可穿戴的艺术作品。这就是我的企业Hanusa Design背后的想法。我制作独特的产品,这些产品的特点是以数学的美丽和精确为灵感的惊人设计。这些作品是利用Wolfram语言中的一系列功能创造的。正好赶上情人节,我们最近在Wolfram商店推出了Spikey耳环,有镀玫瑰金的黄铜和红色尼龙两种颜色。在这篇博客中,我将给大家介绍一下其背后的故事,并讨论一个想法是如何通过Wolfram语言变成产品的。
首先,我们将通过教程来了解如何创建一对数学耳环。在这篇文章的下半部分,我会分享我最喜欢的一些设计背后的数学和Wolfram语言命令。
制作一对十二面体耳环
Hanusa Design的每件产品都在Wolfram Mathematica中进行了3D建模,然后进行3D打印,使珠宝成为现实。许多设计的核心是多面体几何,在Wolfram语言中可以通过PolyhedronData命令轻松访问。例如,这里是一个十二面体。

PolyhedronData还将多面体的顶点、边和面的坐标置于您的指尖,这使得创建十二面体的线框版本变得轻而易举:

在前面的代码中,"EdgeIndices "指的是构成边缘集的顶点对。我们需要使用 Tube 命令来创建线框的边缘,并使用 Sphere 命令来完成角的制作,以便使结果可以进行 3D 打印。该模型已准备好导出为3D打印机所需的格式之一。

现在可以将得到的文件进行3D打印了。然而,此时我们可能应该注意对象的尺寸和精加工。我发现,重新导入STL文件是确保Mathematica工作时使用良好对象的方法之一:
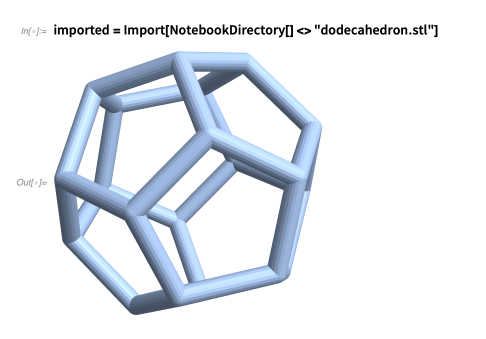
导入的模型是一个MeshRegion对象,这意味着我们可以应用区域变换命令。例如,STL文件的标准尺寸是以毫米为单位的,所以如果我们想要一个宽度为2cm的十二面体耳环,我们应该将导入的区域调整为20mm宽:

虽然可以直接将耳线连接到这个线框十二面体上,但我更喜欢为此添加一个专门的环。我还将使用TransformedRegion和RotationTransform两次来旋转我们的调整大小的模型,这样就可以在多面体的顶部连接环。小贴士:我通过将ArcTan应用于y坐标为零的十二面体顶点,找出了在y轴上旋转它所需要的角度。

通过使用ParametricPlot3D命令绘制一个圆形路径来创建环形。通过使用Tube作为PlotStyle选项将其转换为环形路径。指定PlotPoints的数量可以确保环形是平滑的,而不是多面的:

由于我们已经将一个区域与ParametricPlot3D对象混合在一起,我将导出并重新导入,这样我就可以用TranslationTransform制作第二个耳环副本:

3D打印珠宝似乎占据了3D打印的甜头。当一件作品使用选择性激光烧结打印在尼龙中时,它的价格低廉,并且可以被染成明亮和醒目的颜色。通过失蜡铸造法制作金、银或黄铜材质的作品。将高分辨率的蜡模型进行3D打印,在其周围形成石膏模具,然后用熔融的金属代替蜡。尽管金属打印的价格比尼龙贵,但由于模型的尺寸,它们仍然是实惠的。要知道,对于3D打印的物体,如果你把模型的比例放大2倍,那就会使材料的体积(因此成本)增加8倍!
用Mathematica创建的数学珠宝
现在,我们已经一起制作了一些耳环,并探索了一些关键功能,我很高兴与大家分享我的一些数学灵感的珠宝作品,所有这些作品都是使用Wolfram语言进行3D建模的。
3D打印可以实现复杂的设计,而这些设计用其他方式是不可能实现的,比如当它们由互锁件组成时。我一直以来最畅销的一些设计是这些悬垂的立方体耳环和与之相匹配的联锁八面体项链。我小心翼翼地将这些形状排列起来,使其相互交错,并优化它们的几何形状,以降低印刷成本。

在过去的节日里,我的新Mobius项链给人留下了深刻的印象。它的创作涉及到为Mobius带子制作一个自定义的数学函数(ParametricPlot3D在这里很有帮助),并在其边界上仔细地选择点,使三角形美观。

这个泡泡吊坠是一件生成式艺术作品,这意味着我设计了一种算法,将环放在随机的位置,并给它们随机的半径,但没有指定它们的最终位置。当然,我大量使用了RandomReal函数。在Wolfram社区的这篇帖子中阅读更多关于这个挂件的内容。

我的一个新作品是这个基于阿波罗圆包装数学的系列。这样的排列开始时有四个圆,它们都在一个点上互相接触(外圈和三个内圈)。其余的圆是通过去掉四个圆中的一个,并找到一个与其他圆相触的替代圆来生成的。这个过程可以无限期地继续下去,圆圈越来越小。充满气泡的阿波罗尼亚耳环是一对错配的耳环,最初选择的圆圈是随机的。它们之所以有气泡感,也是因为最外面的圆圈被去掉了。

使用阿波罗项链时,佩戴者的颈部位于最大的内部圆的位置。圆圈替换过程在Mathematica中自动进行,直到所有大于给定截止值的圆圈都被包括在内。

有时候,我遇到了一个似乎太有趣的概念,不能不做。这些大胆而独特的Rotini耳环就是如此,因为它们的形状像意大利面,所以被称为 "Rotini"。这些圆柱形耳环是根据数学函数的图形,如抛物线、指数函数和锯齿函数,围绕中心轴旋转加号(+)的形状而制作的。

美学灵感的另一个来源是分形的数学。它们的迭代性与在Mathematica中进行编程是完美匹配的。以下是我以Koch四面体(一种三维分形)为基础的耳环。您可以从一个四面体开始,在四个面的每一个面上,您都可以建立一个更小的四面体。这个新的形状有更多更小的三角形边,在每一个三角形边上,你都会建立一个更小的四面体。对于这个设计,我到此为止,但如果你继续下去(放置越来越小的四面体),你就会拥有整个分形,这将是科赫雪花的三维模拟。令人惊讶的是,这个分形的极限形状完全适合于一个立方体。

这些骑士之旅耳环是我个人的最爱。我喜欢适合耳环的黑白国际象棋主题,因为它们是3×3×3立方体中两个不同的骑士之旅。我在Mathematica中创建了一个马步图,并使用FindHamiltonianCycle找到两个明显不同的马步图。我还不得不使用一些三角法将立方体立在它们的角上。

我最早的一些作品是这些基于总是令人赏心悦目的Voronoi图(可通过VoronoiMesh函数获得)的吊坠。蜂窝状吊坠需要将Voronoi图与其他形状相交。(RegionIntersection在这里很有用)。

斐波那契雪花吊坠中定义Voronoi图的点位于斐波那契螺旋线上。
我将以一个可以盯着看几个小时的设计来结束这次摄影之旅:我的内省项链。这个吊坠的灵感来自于四维空间;如果你仔细观察,你可以看到它是由两个超立方体组合而成的。我发现三维设计需要思考可见的层次,以及设计的哪些部分阻挡了设计的其他部分。能够部分地看透一个对象,使得对象更加复杂和吸引人。
京ICP备09015132号-996 | 网络文化经营许可证京网文[2017]4225-497号 | 违法和不良信息举报电话:4006561155
© Copyright 2000-2025 北京哲想软件有限公司版权所有 | 地址:北京市海淀区西三环北路50号豪柏大厦C2座11层1105室