Wolfram | Alpha中的分步数学工具帮助您的化学课程预习

Wolfram | Alpha中的分步数学工具帮助您的化学课程预习

数学是阻碍学生想要学习更多化学知识的主要原因之一。作为一名化学工程专业的学生，我理解这一点，特别是对于那些只需要把化学作为通识教育要求的学生来说。从本质上讲，分步解决方案就像你自己的按需数学导师：除了计算答案，Wolfram|Alpha还向你展示它是如何实现的。这里有六个重要的数学技能，你一定会在化学课上经常使用，以及它们与不同化学概念的关系。

1. 基本代数

很多化学技能都涉及到基本代数的应用。然而，大部分代数都隐藏在 "反应物"、"生成物"、"摩尔"、"摩尔数 "等花哨的化学词汇背后。如果你仔细阅读这些问题，你会发现大部分工作其实只是一道代数题。

首先，我们来看一个表达式，复习一下平衡常数、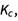，问题中可能出现的代数技巧。简化下面的表达式。(x + 1) - 2(x2 + 10 * x). 这是通过将负系数分配到括号中的所有部分，结合同类项，并从指数最高的项到指数最低的项进行排序。在Wolfram|Alpha中，如果你输入 "简化(x+1)-2(x^2+10*x)"，你可以找到这个步骤的解决方案：

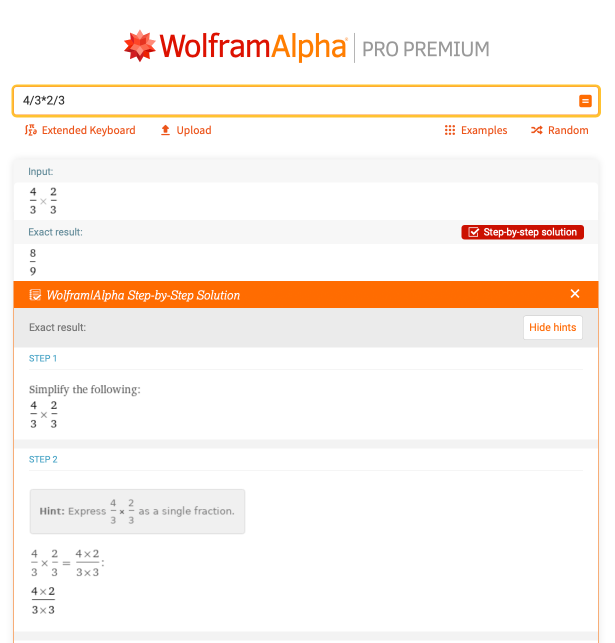
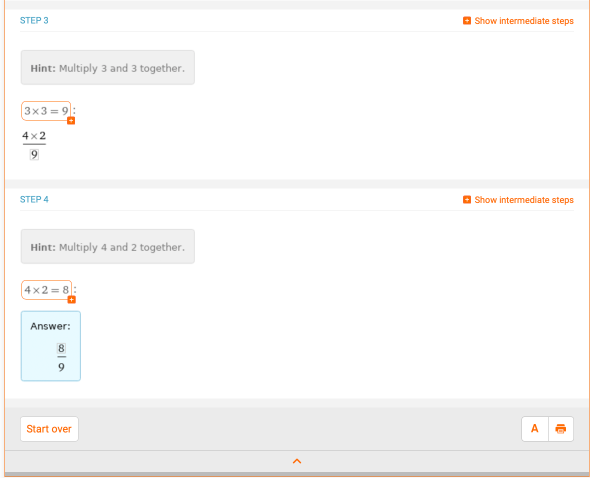
分数是另一个在化学中会经常见到的东西，特别是在化学中的计量问题中。我们来看看一个基本的分数乘除法的例子。4/3*2/3的解决方案是什么？Wolfram|Alpha提供了一个全面的分布解决方案，作为对分数乘法的复习：

接下来，我们来看看一道使用分数的化学题。这可能是你现在看起来不熟悉的东西，但很快就会了! 考虑化学反应AlCl3 + NaOH -> Al(OH)3 + NaCl。假设你有2摩尔的AlCl3，那么你可以通过运行反应来完成多少摩尔的NaCl？那么，你可以在Wolfram|Alpha中输入 "2摩尔AlCl3 + NaOH -> Al(OH)3 + NaCl"：

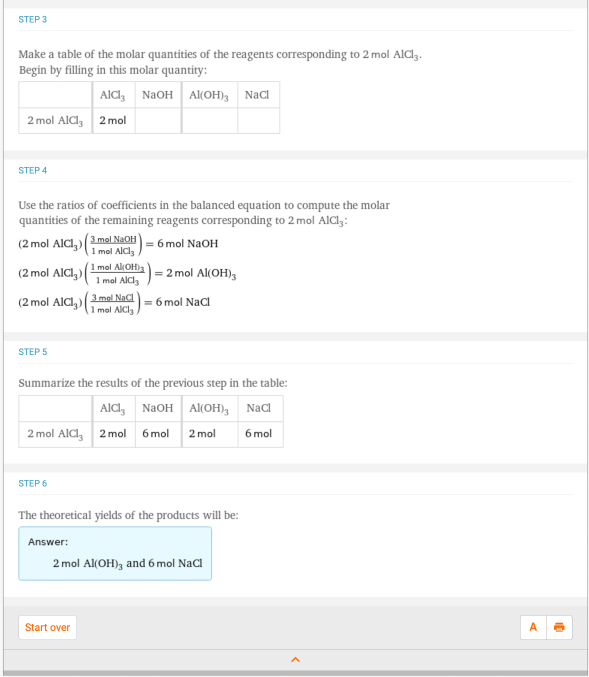
从化学计量步骤的结果来看，我们可以看到，答案应该是6摩尔的NaCl。再看第四步，你的方程渐渐减少到*=6摩尔的NaCl。没有一开始看起来那么糟糕吧？

2. 单位换算

每个化学学生最可怕的噩梦：单位换算，比如从厘米换算成米，毫升换算成升等等。但仔细想想，这些都是分数而已，我们在上一节已经讲过了。这也是学生第一次化学考试最容易出错的地方之一，通常是以乘代除，或者反之。除此之外，化学中的大部分单位都是公制单位，也就是SI单位，对于生活在美国的人来说，可能比较陌生。

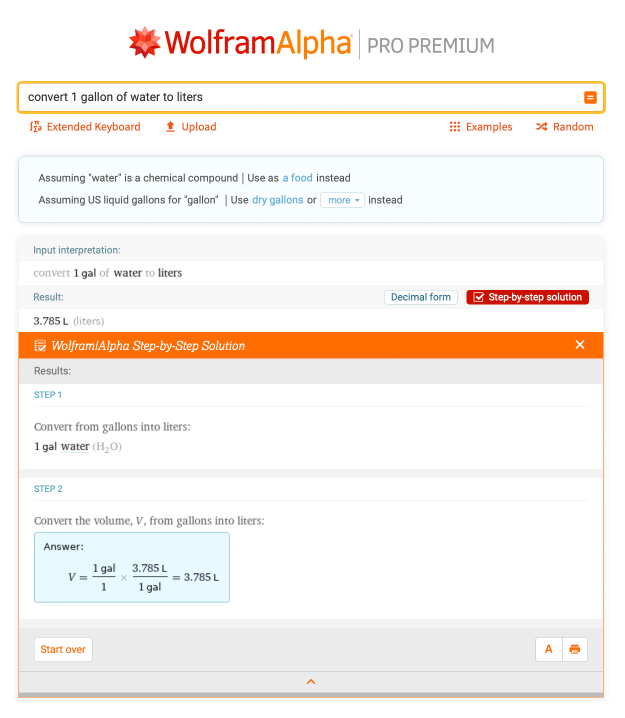
我们先用一个比较熟悉的单位：加仑。让我们把一加仑的水换算成升。通过输入 "将1加仑的水换算成升"，我们看到它等于3.785升。利用这个知识，如果你有两加仑，你可以将3.785乘以2，得到7.571升：

我们来看一个常见的化学换算：将质量换算成摩尔。这是你在化学中会遇到的许多维度分析问题之一。你刚刚在实验室的天平上测出了10克蔗糖，但需要知道你有多少摩尔的蔗糖。你可以在Wolfram|Alpha中输入 "10克蔗糖转摩尔 "来进行这个转换：

3. 求直线的斜率和截距

化学家们特别喜欢线性关系，其中非常流行的是比尔-朗伯定律实验的基础。利用分光光度计收集到的已知浓度样品的数据，可以形成一条最佳拟合线，这也叫线性回归。这个方程的形式是y=mx+b，其中m为斜率，b为y截距。

通过一个简单的方程，如y = 3x + 1，确定斜率和截距是什么将是有帮助的，因为这些值可以插入其他方程或解释以确定特定的趋势或相关性。例如，如果斜率是负的，那就意味着存在逆相关，而正的斜率则具有直接的相关性。

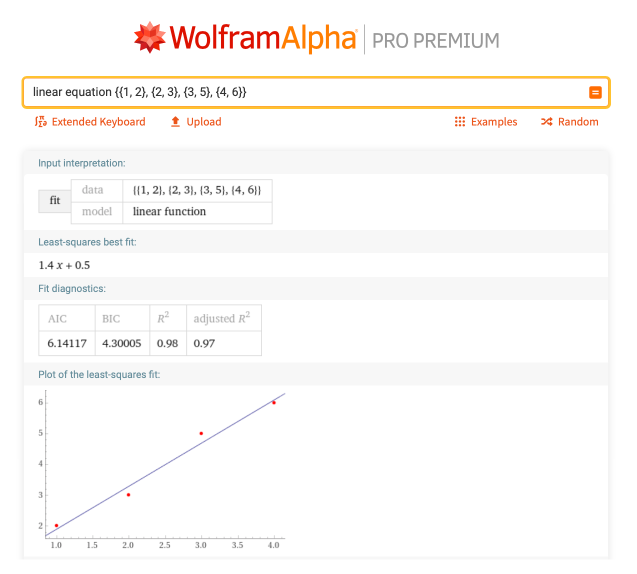
给定一个点的列表{{1，2}，{2，3}，{3，5}，{4，6}}，Wolfram|Alpha可以确定最佳拟合线性方程："线性方程{{1, 2}, {2, 3}, {3, 5}, {4, 6}}"。

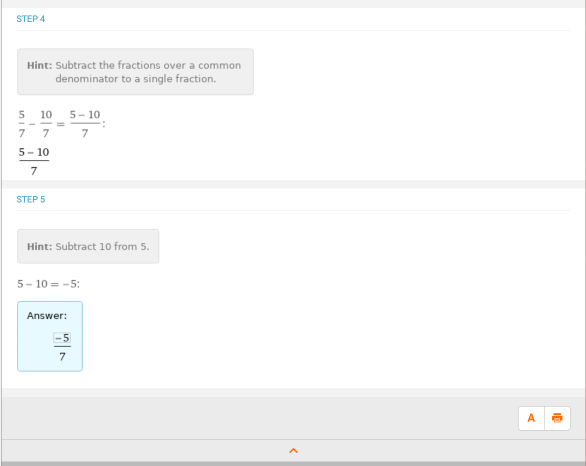
此外，Wolfram|Alpha还可以用来重写一个不是y = mx + b形式的方程，将其变成这种形式。例如，给定方程 2x + 7y - 5 = 0，斜率和截距是多少？只要输入 "求解2x + 7y - 5 = 0 for y "即可：

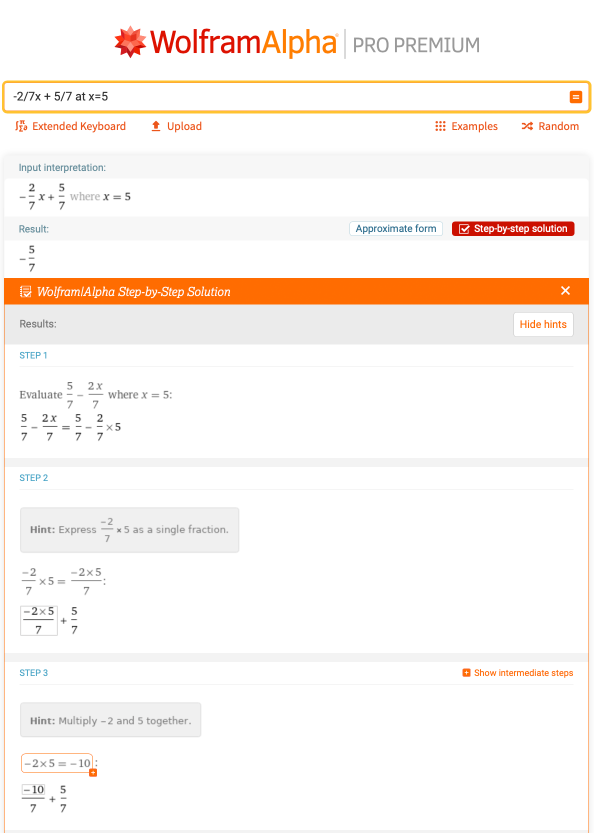
斜率为m=-2/7，y截距为b=5/7。你也可以输入 "2x+7y-5=0的斜率和y截距"，直接得到答案，但知道如何确定方程的斜率-截距形式中的每个部分是很有帮助的。继而，如果有人要问给定x=5，y的值是多少，通过计算x=5时的-2/7x+5/7，答案是-5/7，可以用前面看到的基本代数技巧来计算：

能够识别斜率和y截距是什么，还能插值确定y是什么，对于化学中的题目，比如动力学，是一项非常重要的技能。

在化学中，我们用摄氏度来测量温度，而不是华氏度。给定几个已知的摄氏度和华氏度的温度，我们如何在不使用数字助手的情况下转换其他温度呢？好吧，我们以五点为例，其中的搭配会列成{华氏、摄氏}。{{40, 4.4}, {50, 10}, {60, 15}, {70, 21}, {80, 26}}. 我们可以用 "线性回归{{40，4.4}，{50，10}，{60，15}，{70，21}，{80，26}}"找到这条线的信息：

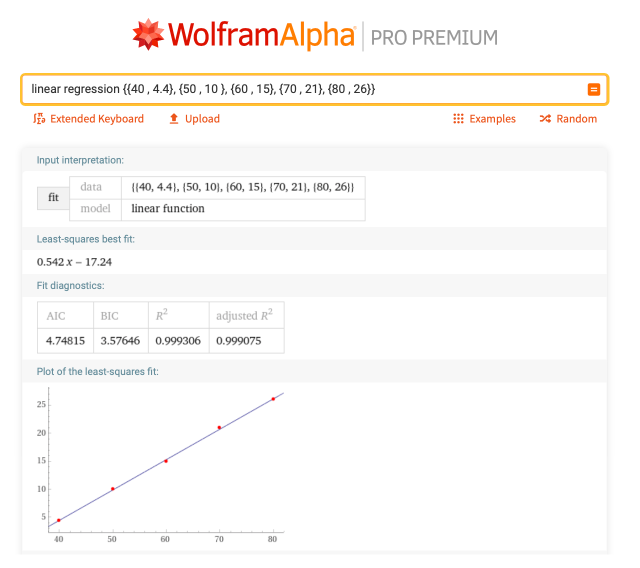
这条线的方程是y = 0.542x - 17.24，其中x是华氏度，y是摄氏度。因此，如果你有一个摄氏度或华氏度的值，你可以通过将该值插入这个方程，然后求解另一个变量来转换为其中之一。所以，如果你想从华氏度转换到摄氏度，当然只要输入 "75华氏度到摄氏度 "就可以了，但是能够看到这种线性关联，即使你不能访问互联网，也能帮助你确定这种转换。

4. 求解x

要想在第一堂化学课上取得成功，还需要一个重要的概念，那就是如何用逆运算来求解x。将数字和变量重新排列，以隔离x，并确定未知值，在求解不同的值，如能量、质量、体积等方面是如此重要。

我们举个例子，用乘除法求x，给定方程8*x=3*0.08206*298，x的值是多少？这其实是直接从理想气体定律中提取的方程，并插入了数值。理想气体定律问题可以让我们求解压力、体积、物质的量和温度。在所有的情况下，努力归纳出一个有x的表达式来求解。组合项后，Wolfram|Alpha通过 "求解8*x=3*0.08206*298为x "来解决。

我们可以将理想气体定律计算器的结果纳入例题。确定1摩尔甲烷气体在150开尔文和1大气压下的体积：

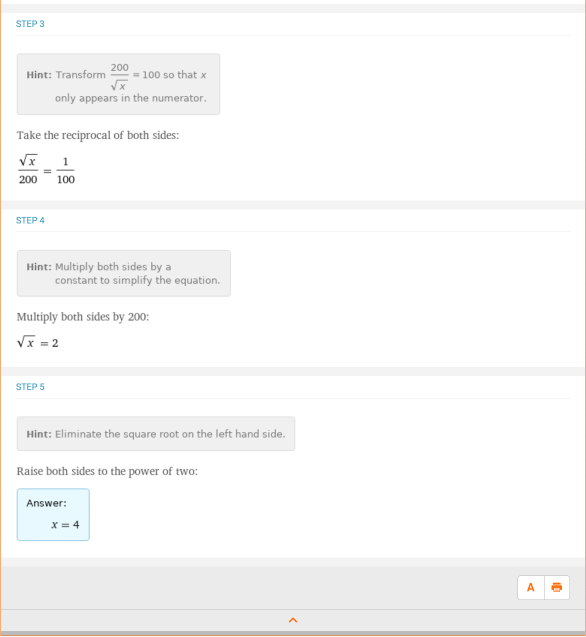
下面是另一个使用指数规则的问题。"求10^2=200/sqrt(x)时的x"。将102简化为100后，剩下的步骤如图所示，这样就可以很好地复习使用指数来隔离变量：

我们来看一个更复杂的例子。这个涉及到二次函数中x的求解，它出现在平衡和缓冲问题中。给定0.0125=(x)*(x+0.1)/(3-x)，那么x是多少？这个用手做就难多了，我们来看看Wolfram|Alpha对 "解0.0125=(x)*(x+0.1)/(3 - x) "的说明：

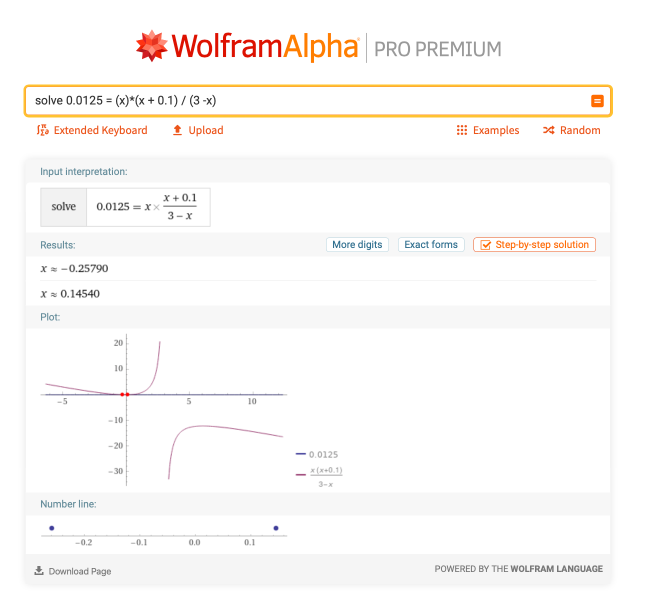
这道题也有分步解法，但点击近似形式按钮后的两个答案是x=-0.25790和x=0.14540。这在化学中是非常有用的，特别是在求解平衡反应时。然而，在化学中任何涉及方程的地方都会遇到求x的解。

5. 对数

大多数情况下，在解决酸碱问题时，对数是用计算器计算的，但知道如何使用对数是很有帮助的。在化学中，主要使用的对数类型是碱10和碱e，或者自然对数（计算器上的ln按钮）。除非对数等于一个整数，否则你可能需要使用计算器来解决这些问题。关于对数的一个重要概念是如何从指数形式到对数形式来回切换。例如，log10(100)=2的指数形式是什么？应该是102=100。鉴于这个例子，你应该能够确定一个变量的值，给定一个对数问题。例如，在 log10(x) = 4 中，x 的值是多少？Wolfram|Alpha有一个很好的分布解决方案：

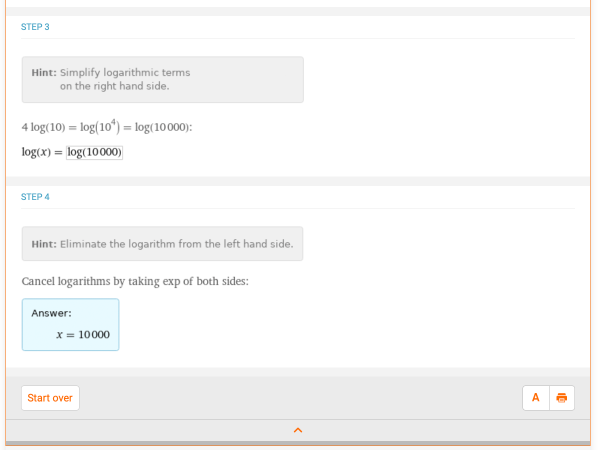
对数主要用于pH值的计算，因为pH值是以10为基数来衡量的，也就是说，pH值为3的比pH值为4的要 "强 "10倍，也就是说，很多时候你最终得到的pH值不是一个整数。你也可以使用Wolfram|Alpha来计算一些手工计算比较困难的对数，比如方程log10(x)=3.5中的x值。"求解log10(x)=3.5 "产生的答案是3162.3，点击小数形式按钮后，如图所示：

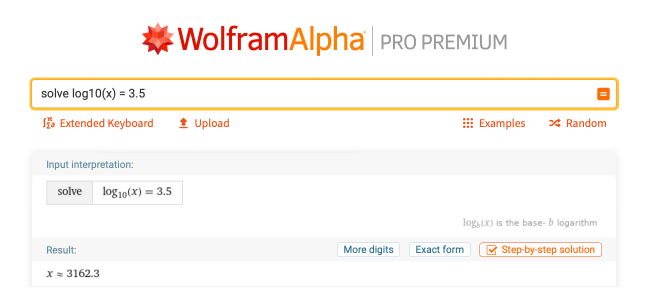
这道题的解题过程与上一道题类似，但小数指数的计算非常困难，所以使用计算机或计算器来确定这个答案是必要的。另外值得一提的是，Wolfram|Alpha中的log(x)并不是解释为基数10，而是自然对数。如果你需要基数为10，一定要输入log10(x)。

6. 寻找二次方程的根数

第一次化学课程要知道的最后一个重要概念是二次方程的求根。二次方程的形式为a * x2 + b * x + c = 0，x的值由-b ± Sqrt[b2 - 4ac]/2a给出，这就是所谓的二次方程。当然，这样的解根常常会把人绊倒，但用计算机来帮你解，就快得多，也准确得多! 在化学世界里，求二次函数的根，在解决平衡问题，特别是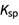方程，通常没有分母，是很有用的。

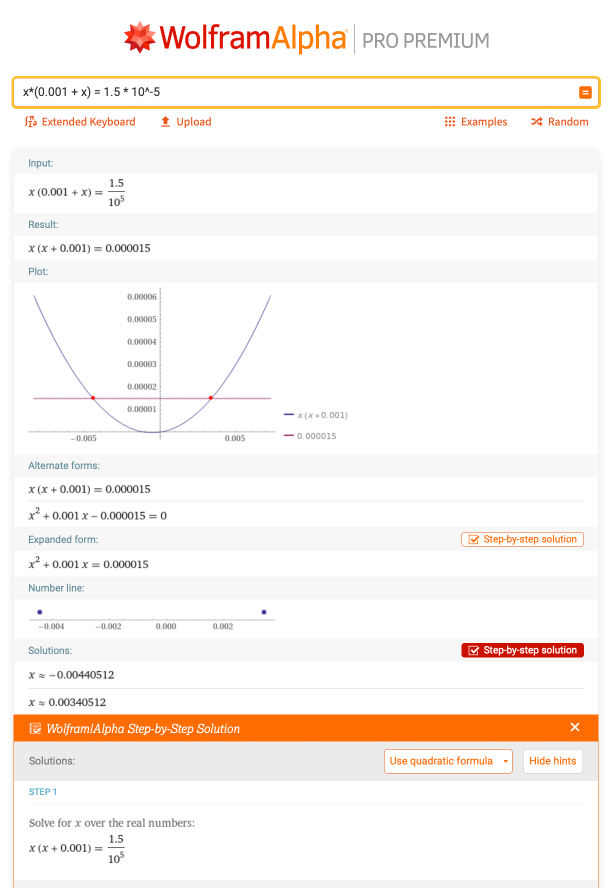
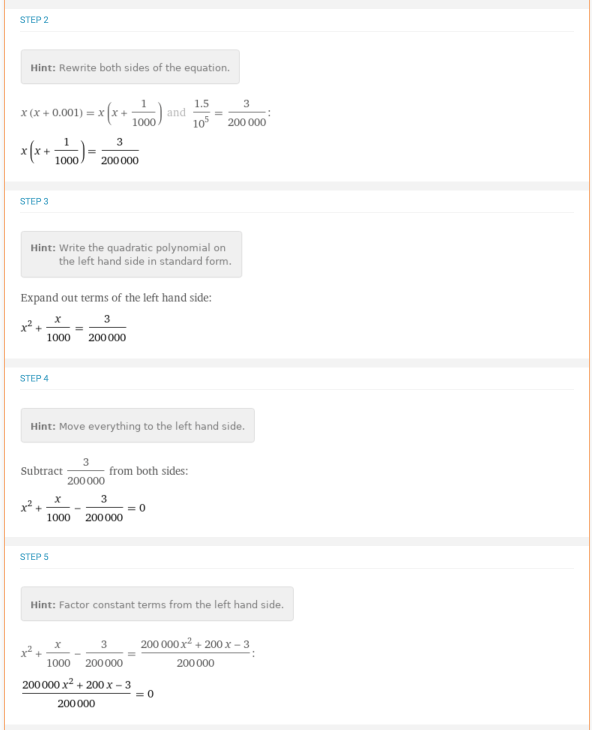
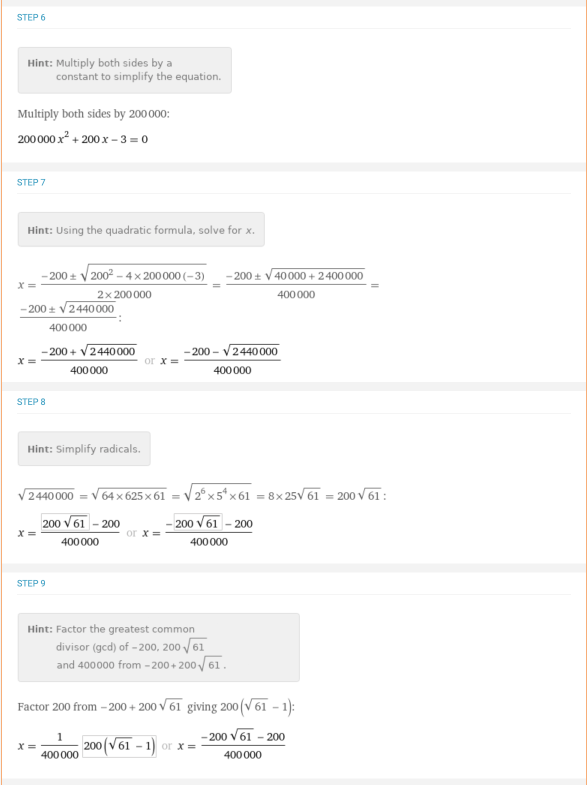
考虑到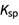问题：你需要解决方程x*（0.001+x）=1.5*10-5的根。这种情况下，就必须先重新排列项，使方程等于0，然后再使用二次方程。这个问题有详细的分布解决方案：

有时，在你的作业题中可能会出现含有立方项的方程，如x3，以及更高的方程。例如，x3 - x2 + 9 * x - 9 = 0，在这种情况下，x的值是多少？Wolfram|Alpha将通过输入 "求解x^3 - x^2 + 9 * x - 9 = 0 "来确定根：

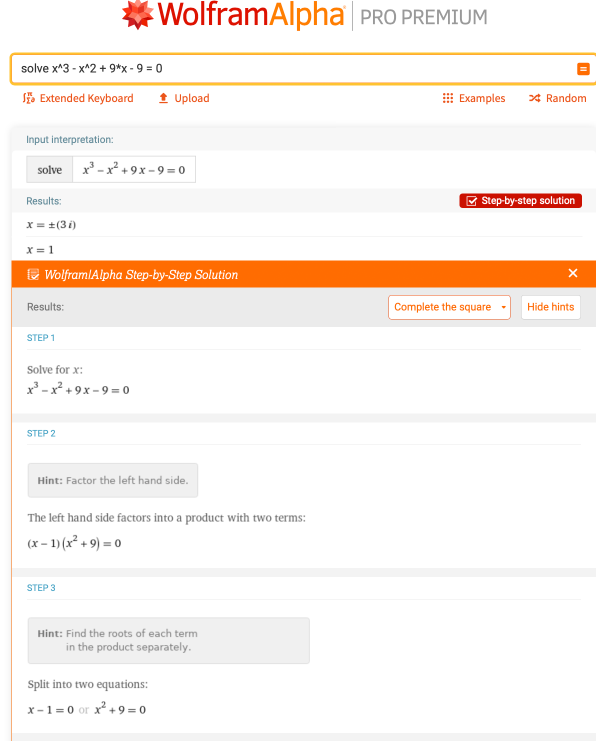
请记住，除了二次方程外，还有更多的方法可以解方程的根。Wolfram|Alpha提供了不同类型的分步解题方法，无论是因式法、二次方程还是完形方程，都能教你手把手地解决同一个方程。

数学与化学携手并进

当你学习更多的化学概念时，你可以看到数学与化学是如何交织在一起的。它真的很美，所有的东西最后是如何结合在一起的，但重要的是要对背后的代数感到满意，才能看到其中的联系。我推荐大家使用Wolfram|Alpha Pro来解决数学和化学的问题，因为很多问题都会给你提供分布解决方案，这可以帮助你在化学课上获得很大的成功!