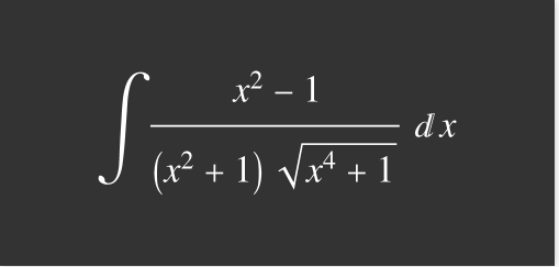
2004 年,我开始沉迷于计算积分,使用微积分学生已知的基本技术和 Davenport、Trager 和 Bronstein的Risch 算法及其扩展 [1, 2, 3, 4, 5]。从George Beck的分步微分程序WalkD 中获得灵感,我决定编写一个计算不定积分的分步程序。
例如,很容易在Mathematica 中编写一组简单的替换规则来对(扩展的)多项式进行积分:


使用这些规则,我们现在可以对多项式进行积分,例如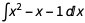 :
:




在花费太多深夜将集成技术作为模式匹配规则输入 Mathematica 之后,我使代码处于合理状态,并将其发送给Wolfram Research,以便可能将其包含在 Mathematica 中。不久之后,我 在Wolfram得到了一份工作,在那工作了几年,主要致力于Wolfram|Alpha。我的逐步积分器仍在计算许多积分,其中一些我自己很可能已经忘记了如何做。
顺便说一句,使用基于规则的编程来计算不定积分的想法可以追溯到 1961 年,当时麻省理工学院的 James Slagle使用符号自动积分器(SAINT)。SAINT 可以解决“大约相当于优秀大学新生水平的符号整合问题,事实上,它使用了许多与新生相同的方法(包括启发式)”[6]。我编写的逐步积分器使用了大约 350 条规则,可以对微积分教科书中 99% 以上的积分进行积分。从那时起,Albert Rich 使用 Mathematica 创建了基于规则的积分器(Rubi),它使用了超过 6,700 条规则。
快进到 2020 年,我已经有十年没有研究过积分了。我决定看看过去 10 年左右取得了哪些进展。我对Manuel Kauers 开发的基于Gröbner 基的算法及由 Brian Miller 开发的扩展特别感兴趣,该算法在 AXIOM 计算机代数系统中的许多积分 [7, 8] 中似乎可以胜过 Risch 算法的代数情况。例如:
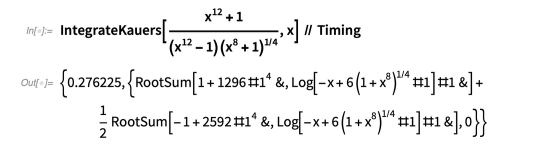
检查结果很简单:
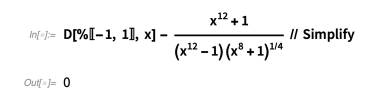
再一次,我很快就迷上了积分,或者更具体地说,是不定积分的算法解决方案。
当我最后一次查看符号积分时,我对 Risch 算法的先验情况感兴趣,其中 Mathematica 有一个近乎完整的实现。例如,下面是 Risch 算法先验情况的简单积分:
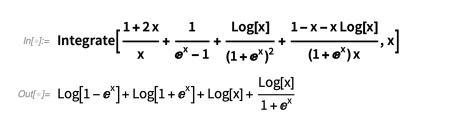
我对代数积分更感兴趣,它不能与先验 Risch 算法集成。Risch 算法的代数情况比先验情况复杂得多,并且尚未在任何计算机代数系统中完全实现。
我最初考虑了许多微积分教科书中出现的代数积分:
|
|
如果我们很乐意通过分支切割快速而宽松地完成,那么我们可以将这个积分写为:
|
|
对于这个积分,我们可以替换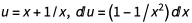 ,我们得到:
,我们得到:
|
|
代入,我们得到:
|
|
这个答案有分支问题;但是,我们可以通过将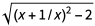 写为
写为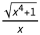 来解决此问题。那么我们就有了正确的反导数:
来解决此问题。那么我们就有了正确的反导数:
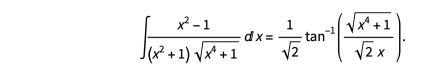
我想知道这种使用Laurent 多项式替换来简化代数积分的方法是否只是适用于该积分的技巧,还是对更通用方法的提示。事实证明,这个技巧适用于许多积分;例如,我们之前在 Kauers 算法中尝试的积分
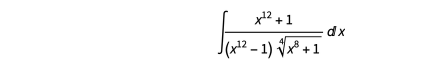
可以减少到

替换为u = x 4 + x –4。一旦纠正了分支切割问题,解决方案如下:
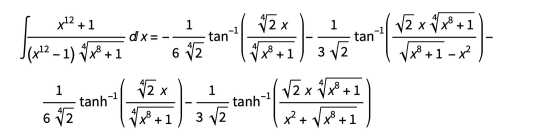
一般方法会寻求形式u =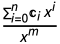 的替代, 例如
的替代, 例如
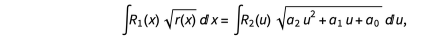
其中R1(u), R2(u)是u的有理函数,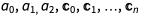 是待定系数。
是待定系数。
我们首先使用SolveAlways来计算u替换中的待定系数:
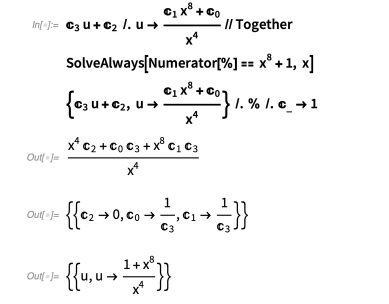
所以我们有一个适合被积函数的基数部分的候选替换。这个替换是否适合被积函数的其余部分?我们可以这样计算:

我们对之前手动做的积分做了同样的简化,即
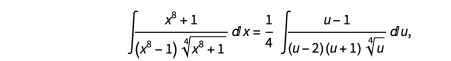
其中 u = 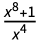 .
.
这个方法是在Wolfram函数库中用IntegrateAlgebraic实现的。 (在2020年,我进一步研究了用初等函数[9]计算伪椭圆积分。) 由于这种方法简单,它适用的积分范围很广。
下面是一些例子:
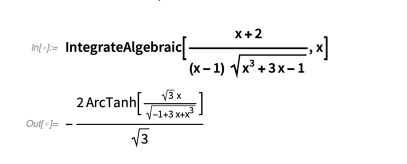
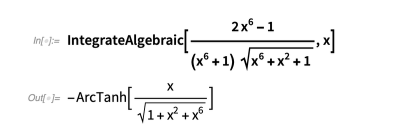
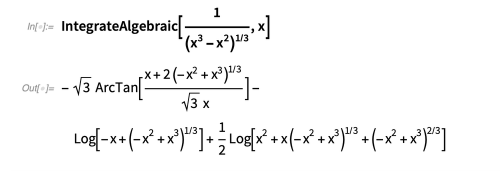

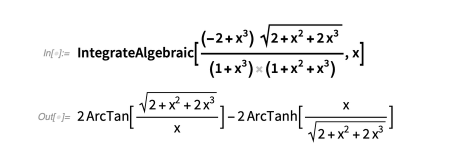
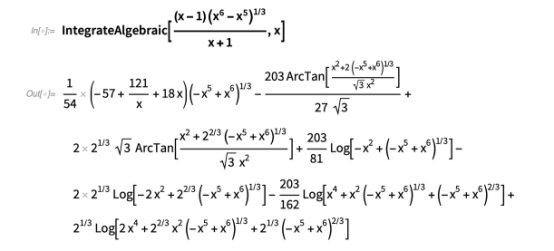
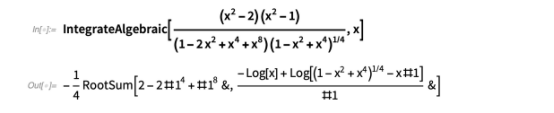
与 Risch 算法的代数情况不同,该技术可以快速求解许多涉及参数的积分:






下面的积分呢?
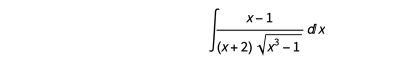
与前面的例子不同,这个积分不能用 Laurent 多项式替换来求解。
1882 年,Günther 开发了一种计算一些困难的代数积分的方法 [10]。比如积分
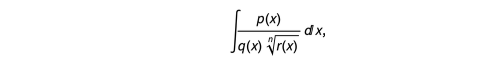
p(x)和q(x)是x的多项式,Günther做了替换
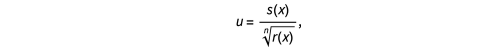
使得积分变为
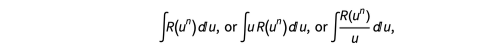
其中 s(x) = vQ–P+R–1 xQ–P+R–1 + vQ–P+R–2 xQ–P+R–2 + … + v1 x + v0, 其中P = degx(p(x)), Q = degx(q(x)), R = degx(r(x)) and v0, v1, …, vQ–P+R–1, c0, c1,c2, c3 是待定系数, R(un是系数未定u n 中的有理函数。
我们可以使用 Günther 的方法来解决 Mathematica 中的这个积分,如下所示。替换的形式为:
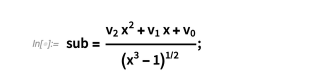
我们假设u 中的被积函数具有以下形式:
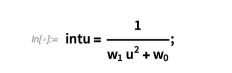
那么x 中的被积函数由下式给出:
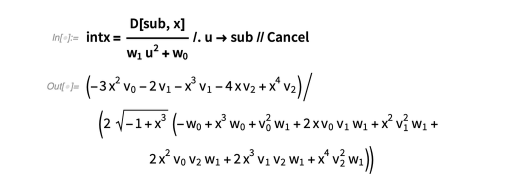
现在我们需要求解代入 ( v 0 , v 1 , v 2 ) 和有理被积函数 ( w 0 , w 1 ) 中的未定系数:

我们可以把这个解代入u中的被积函数,然后替换

现在我们可以使用integral来计算得到的积分:

然后代回求解我们原来的积分:
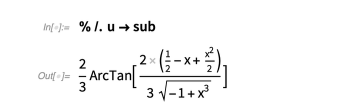
快速检查我们的解答是正确的:
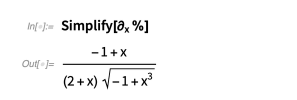
Günther方法的一个推广版本在IntegrateAlgebraic中实现。 这种方法可以解决许多比较困难的积分。 下面是一些例子:
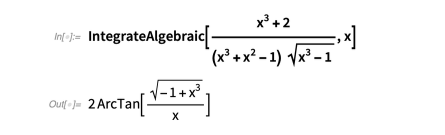
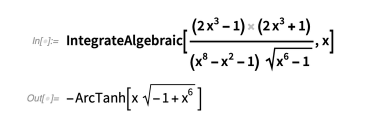

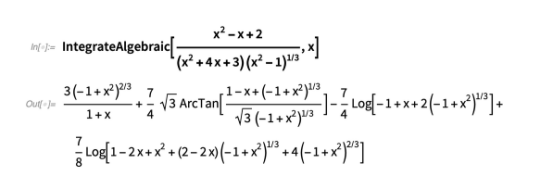
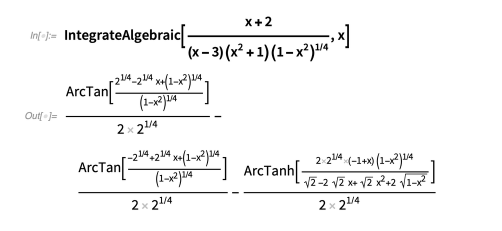

此方法还处理包含参数的积分:
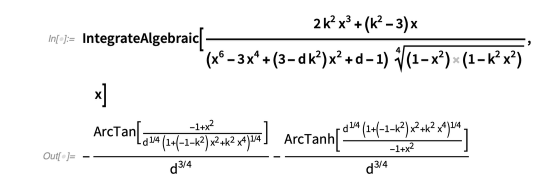

如果我们在将被积函数扩展为项的总和后将这种方法与逐项积分相结合,我们可以处理更多奇特的代数积分:

将 Laurent 多项式替换方法与广义 Günther 方法相结合并逐项积分,我们可以计算更复杂的积分:
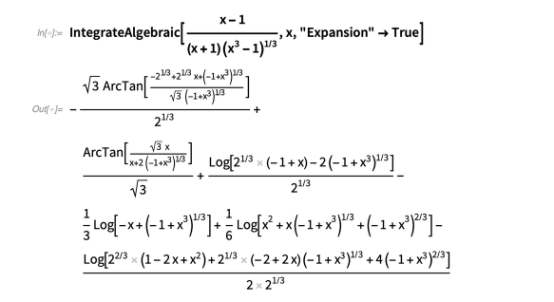
在这种情况下,我们将积分写为:
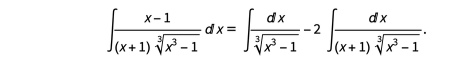
然后积分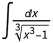 减少到
减少到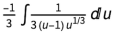 代入u = 1 – x 3,而积分
代入u = 1 – x 3,而积分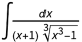 减少到
减少到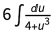 代入s =
代入s = 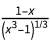 。
。
积分包含嵌套基元的表达式一直是一件棘手的事情。 一个众所周知的例子是
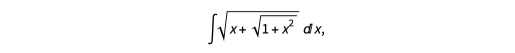
可以使用替换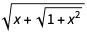 来计算。我们可以用GroebnerBasis进行这种替换,如下所示:
来计算。我们可以用GroebnerBasis进行这种替换,如下所示:
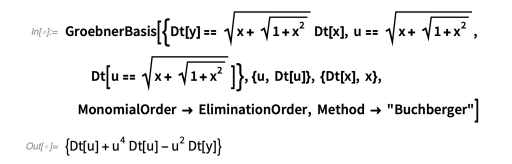
我们需要用Dt [y]来表达这种关系:

我们现在可以整合u的有理函数并代回x:
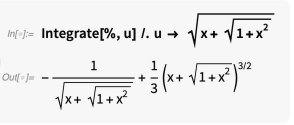
这种方法可以解决更困难的涉及嵌套根的积分。例如:


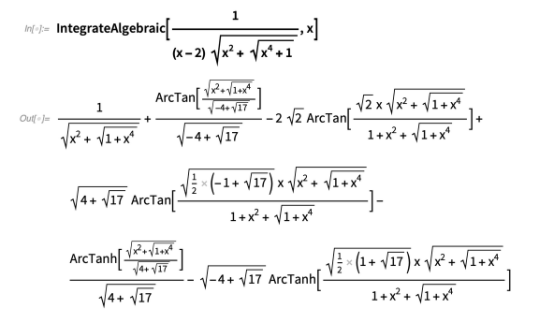
在IntegrateAlgebraic 中使用了这种方法的概括。以下是一些具有挑战性的示例:

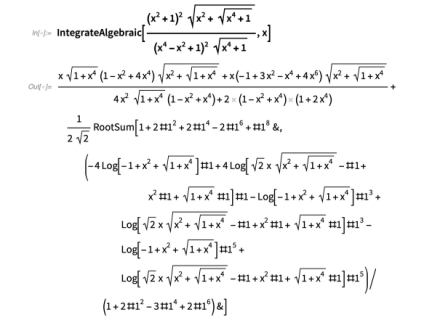
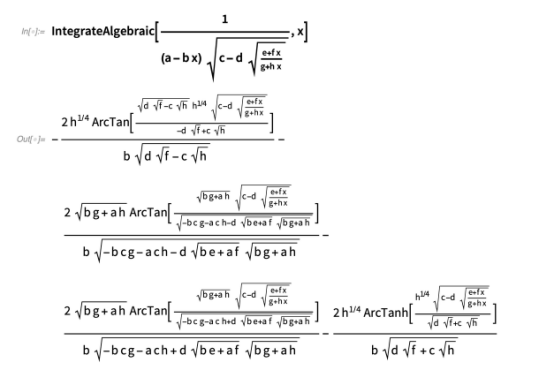
与IntegrateAlgebraic 中的其他方法一样,我们准备好处理涉及参数的积分:
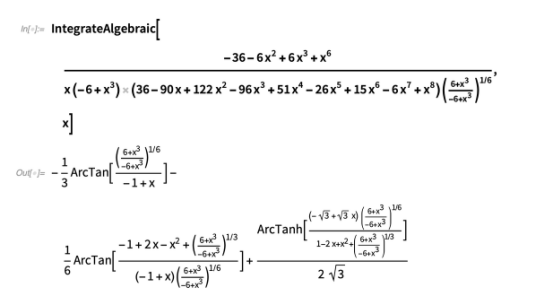
本帖中所有的积分都包含多项式根; 然而,这些方法推广到有理根。 例如:

仍然有许多代数积分是这些方法不能计算的。 例如,下面的积分有一个初等解(尽管解很大):
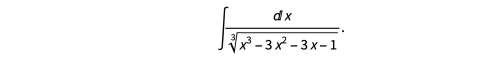
然而,与在任何计算机代数系统中都没有完全实现的 Risch-Trager-Bronstein 算法的代数情况相比,这些方法快速、简单并且补充了 Mathematica 的Integrate函数的现有积分功能。我们目前正在考虑在即将发布的版本Integrate中包含IntegrateAlgebraic。