虽然说 Mathematica 对于很多新手来说还很陌生,或者有用户会说考试里面不能使用,但是在人工智能越来越普及的时代,能够用先进手段帮助我们快速验证想法和复盘已经做过的练习会有相当大的帮助。特别是应用计算机之后产生的直观结果和对于纸面结果的推广和验证,是传统方式难以实现的。下面我简单谈一谈我是如何使用 Mathematica 帮助理解这道问题的。
浅析理科高考压轴如意函数
每到高考结束,语文卷的作文题和数学的压轴题总会得到青睐。它们即使表示考试的结束,也是开启大学之门的钥匙。今年也不例外。有些不同的是,今年的压轴题看上去非常简单,好像随便一猜就有结果。这样一想就中了出题人的圈套了。
原题

解答
对于 a 的取值范围,我们可以首先给 a 划定一个定性的范围,然后扫描一下结果就可以得到一个初步的认知。对原题稍作变化,将不等式右侧移到左侧,那么原问题就是找到相应的 a 使得新的左侧项在 x 不小于零的范围恒大于零。按照我们的直观感受来看,如果 a 很大,那么左侧一定可以是恒大于零。给定一个数字并对 x 在零附近的时候验证一下。因为该不等式左侧包含指数函数,其余都是多项式,所以 x 很大时候就是指数函数。
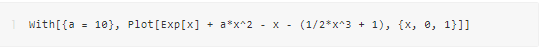
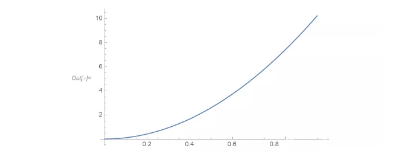
上图符合我们的猜测。那么如果 a 很小呢?剩下的多项式里面可能就不是单调。我们可以改变参数 a 将图像画在两个不同的区间。在原点附近时,函数值为负数;因为指数函数增长很快,逐渐离开原点以后为正。如果 a 继续变小,那么原点附近就会更向下弯曲,所以我们不需要再测更小的参数 a 了。
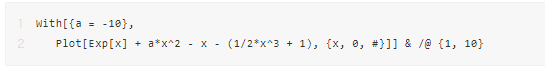
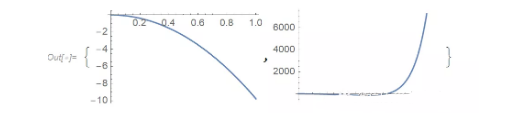 ?
?
接下来我们就可以玩一玩滑动模块来显示我们所要研究的函数究竟是如何根据 a 的变化而变化的。在变化过程中我们也将注意到本问题的真正难点。当 a 不断得从较小的负数增长时,函数的形状回发生四个主要的变化,其中三个都还是保留如意形状。最终形态是单调函数。
 ?
?
图的编号为1至4,从左往右。对于 a 的临界情况来看,应该发生在图 2 和 3 之间:


在滑动 a 至大约 -0.097 的时候,我们可以看到图的结果是在临界位置。
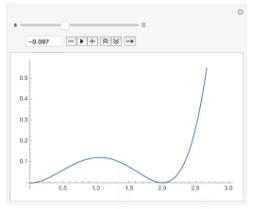
在这个时刻,这个函数出现了两个拐点(大约在横坐标等于 0.5 和 1.5 )并且在 2.0 附近函数与横坐标相切。那么现在我们就可以对这个具体的时刻进行求解。切线斜率:

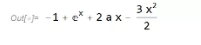 ?
?
联立方程得到实数域上精确结果:

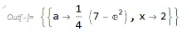
我们又可以验证是否出现我们上图中看到的两个拐点。根据定义我们可以连续求导两次找到凹凸性变化的位置:

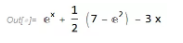
利用数值方法找到具体位置:

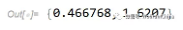
可以最终标记出所有关键位置的点:

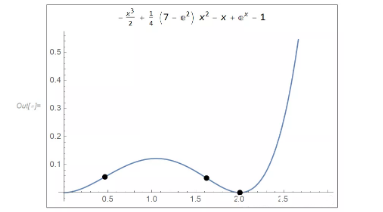
小结
?