Wolfram System Modeler 12.2 刚刚发布，具有诸如图的个性化，新模型库和对高级建模的扩展 GUI 支持等功能。其他功能之一是用于从 3D 形状生成 3D 模型的新工作流程。我们将使用此功能来说明一些奇怪和违反直觉的物理学。
1985年，宇航员弗拉基米尔·德扎尼别科夫（Vladimir Dzhanibekov）受命解救礼炮7号太空站。他解开了从地球寄来的补给品的包装，这些补给品已用翼型|蝶形螺帽锁住了。当蝶形螺母从螺栓上松开时，他注意到蝶形螺母如何在短时间内保持其方向，然后翻转180度。这种“ Dzhanibekov 效应”或网球拍定理至少已有150年了，但是对于我们大多数人来说，它仍然违背常识。是什么导致了这种效果，我们可以重复这种行为吗？
我们需要零重力来复制它，这对我们大多数人来说都是很难做到的。但是，使用System Modeler很容易，所以让我们进行一个虚拟实验。
首先，我们需要一个螺母的几何形状。几乎所有的蝶形螺母CAD模型都可以使用，在这种情况下，我们将使用带有Spikey的巨型蝶形螺母。它的直径约为30米——由于我们将在太空中进行此实验，因此我们不妨变大：
现在，让我们使用新功能从此形状创建系统模型：
CreateSystemModel["Wingnut", wingnut];
就这么简单！现在，我们有了一个模型，它不仅具有所需的形状，而且还具有所需的物理特性，包括惯性、质心和密度。我们只需要将其放在太空中并进行初步移动即可测试Dzhanibekov 效应。我们将以每秒2米的平移速度和每秒10弧度的角速度初始化蝶形螺母：
当然，您也可以在Model Center中以图形方式执行此操作，如本视频(https://wolfr.am/RP7jVEgz)所示。
准备好模型后，我们现在可以模拟：
simWingnut = SystemModelSimulate["DzhanibekovEffect", 30];
由于没有外力，人们可能会期望速度应该保持恒定，但是它们会吗？让我们开始看一下速度：
SystemModelPlot[simWingnut, {"wingnut.body.v_0[1]",
"wingnut.body.v_0[2]", "wingnut.body.v_0[3]"}]
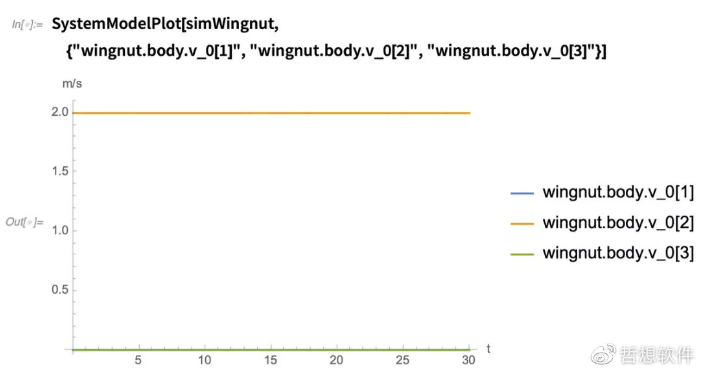
正如预期的那样，它们保持不变，但现在让我们看一下角速度：
SystemModelPlot[simWingnut, {"wingnut.body.w_a[1]",
"wingnut.body.w_a[2]", "wingnut.body.w_a[3]"}]
更容易查看动画的实际情况：
SetSystemModel[
"DzhanibekovEffect", <|
"SimulationSettings" -> {"StopTime" -> 30}|>];
SystemModeler["DzhanibekovEffect", "Animation"]
这恰恰是贾尼别科夫在1985年观察到的怪异效果！由于我们根本没有施加任何外力，因此这种影响（至少对我们大多数人而言）是违反直觉的。是什么原因造成的？从CAD形状创建模型时，会自动计算相应的惯性。让我们看看它们：
simWingnut["wingnut.body.I_11"]
simWingnut["wingnut.body.I_22"]
simWingnut["wingnut.body.I_33"]
它们都是不同的，实际上是由小的干扰（在这种情况下为小的数值干扰）共同导致的。
对象是否将开始翻转取决于我们围绕哪个轴旋转。让我们看一下航天飞机以及它如何根据初始轴或旋转来表现，并使用System Modeler的Simulation Center跟踪航天飞机的三个不同点：
当绕着x和z轴旋转时，航天飞机的行为符合预期，但绕着y和y-z旋转时，它开始以与蝶形螺母相同的奇异方式翻转。当航天飞机以最大或最小惯性矩绕轴旋转时，旋转稳定。但是，当绕中间轴旋转时，惯性矩介于这两者之间，则翻转行为开始。这就是为什么这种效应也称为中间轴定理的原因。
如果您有网球拍或类似产品，实际上可以轻松在家中进行测试。或者，您可以使用Wolfram语言创建一个球拍，并在System Modeler中对其进行测试：
pingpongRacket =
Region[RegionUnion[{Cylinder[{{0, 0, 0}, {0.10, 0, 0}}, 0.015],
Cylinder[{{0.18, 0, 0}, {0.18, 0.005, 0}}, 0.09],
Cylinder[{{0.18, -0.005, 0}, {0.18, 0, 0}}, 0.09]}]]
现在，我们可以将其付诸实践。在这种情况下，我们将停留在地球上，即保持重力：
如果仔细看，可以看到球拍如何翻转。同样，这是由于当对象具有三个不同的惯性矩而围绕中间轴旋转时引起的。
那么，这是否意味着如果我们有一个对称对象，即没有中间轴，那没有问题吗？其实没有，事实证明，空间是学习简单但违反直觉效果的好地方。
当美国于1958年1月31日发射第一颗卫星Explorer 1时，它就很难学到这一点。卫星被设计为绕其长轴旋转，并具有四个柔性天线，如下图所示：
图片来自维基百科
开始时看起来很棒，但是在几个小时内它就开始翻转并开始旋转。与我们之前的示例相反，卫星再也没有向后翻转。相反，它陷入了这种不希望的旋转中。怎么来的？
为了测
试这一点，我们使用圆柱体作为主体创建了一个非常简单的卫星模型，然后使用带有弹簧阻尼器的接头将四个天线（较小的圆柱体）连接到卫星上：
对系统的仿真复制了Explorer 1的行为-更快，因为我们夸大了一些设置：
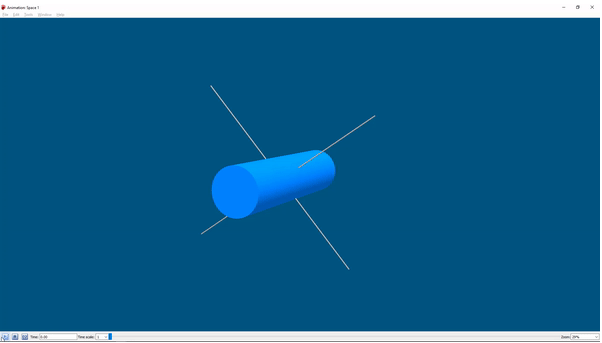
那么为什么会这样呢？弹簧减震器系统会增加系统的损耗。这意味着卫星将寻求绕轴旋转，以实现最小的动能，即具有最大惯性矩的动能，换句话说，当卫星自始至终旋转时。
总而言之，这个简单的例子完全违反直觉，很好地说明了如何使用系统模型来测试和理解动态系统的行为，并希望在设计过程的早期阶段找到更好的解决方案。