1854年,伦敦的Soho 区爆发了一场霍乱,朱迪思·萨默斯(Judith Summers)形容那里到处都是“牛棚、动物粪便、屠宰场、煮油的窝点和原始、腐烂的下水道。” 当时,疾病爆发的原因还不清楚,因为微生物理论还在发展中,疾病传播原理还不清楚。 瘴气理论是当时占主导地位的假说,它提出,包括霍乱和瘟疫在内的疾病是通过有机物分解释放出的恶臭气体传播的。
约翰·斯诺(John Snow)是一名擅长麻醉的内科医生,他设法追踪到疾病爆发的源头是布罗德街(Broad Street)的一个被附近污水坑污染的水泵。 他的方法是绘制霍乱病例的分布图,然后将布罗德街水泵附近记录的感染病例与其他社区的病例进行比较。 这是微生物理论形成的一个重大进展,帮助说服许多科学家霍乱实际上是通过污染的水而不是有毒的空气传播的。
我们还有斯诺的感染病例数据以及他们在Soho 区的位置。在这篇计算性文章中,我们将使用最新的Wolfram语言统计技术和SpatialPointData功能来研究这些数据。
首先,我们将伦敦霍乱的爆发定义为一个空间点配置:

根据斯诺的说法,这些数据包括该地区322座建筑(地点),其中包括被感染的个人(即病例)。 此外,数据还包括每个地点的病例数(病例)、每个地点离布罗德街泵的距离(到受污染泵的距离)和到最近的未污染泵的距离(到无污染泵的距离)。该数据还包含关于布罗德街泵或未受污染的泵是离该地点(最近污染泵)最近的信息。数据不直接使用经纬度坐标,因此泵的坐标必须适当缩放。
现在我们可以以与数据兼容的方式确定受污染的布罗德泵和其他未受污染的泵的位置:

布罗德街泵为红色,未受污染泵为绿色,感染地点在该地区的地图上标明:

每个黑点是一个有一个或多个病例的房子,红色标记是污染泵的位置,绿色标记是未污染泵的位置。
我们可以深入挖掘数据,以显示每个地点的病例数量:
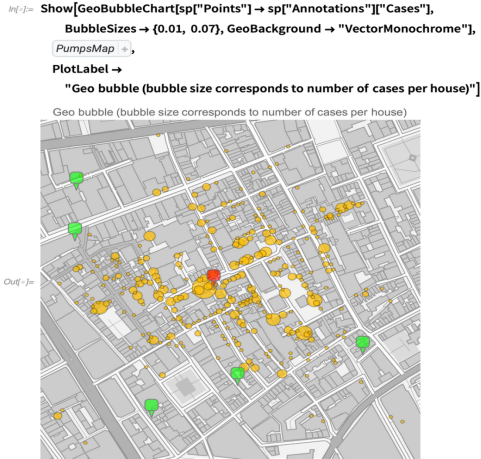
数据中还包含以下注释:

最近的被污染的泵是布尔值,“true”表示被污染的泵是最近的泵,“false”表示最近的泵是未被污染的。
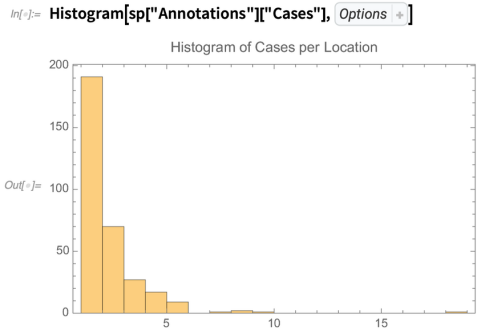
在这个数据集中,每个家庭(以一个点表示)至少有一个霍乱病例。 我们可以创建一个直方图,绘制每个位置的这些病例的数量,以显示比例:
将病例计数与曲线拟合,并绘制它们:

用直方图可视化拟合:

根据获得的分布测试数据:

数据呈负指数增长。 这可能是因为,假设平均每个建筑的感染率相同,每个建筑的人口分布大致遵循这个分布。
如前所述,该数据集还包括到最近的无污染泵和到布罗德街泵的距离,我们现在将探讨这一点。
创建一个未污染和污染泵距离分布图:
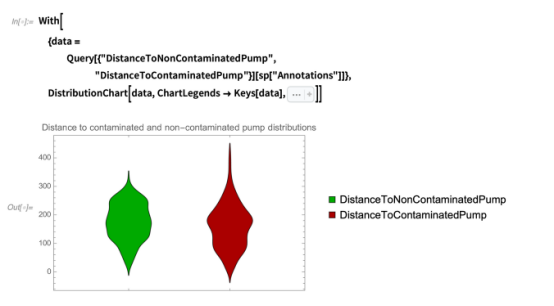
这张图表显示,因为有更多的无污染泵,到它们的最大距离更低。 情况是,平均来说,更接近污染泵,距离污染泵的最小值低于距离不污染泵的最小值。
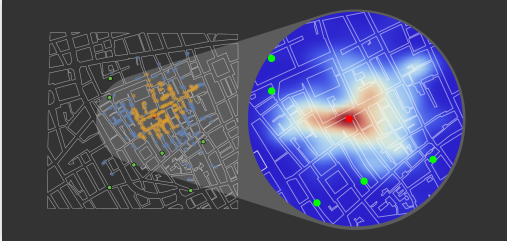
展示病例是如何在空间上分布的:

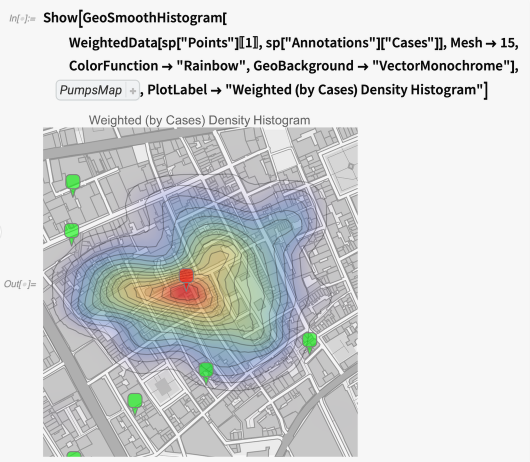
这个平滑的密度直方图统计了每个地点的病例,并创建了该地区病例数量的“密度图”。 这向我们展示了最大的“热点”的形状是一个细长的椭圆形,大约以布罗德街泵为中心,并与街道呈45度角方向。 此外,几乎所有密度高的地区都靠近受污染的泵。 这提供了更多的证据,说明布罗德街泵是导致这些病例的原因。
绘制出距离污染泵和最近的未污染泵的距离分别有多少个点:

请注意,在这些图中,四分位数区间没有重叠。 奇怪的是,似乎有些案例使用了被污染的布罗德街泵,尽管与未受污染的泵的距离更短。 也许这些道路让去布罗德街的水泵更容易,或者人们来这里是出于其他原因?
现在我们要设法找到霍乱爆发的根源。 首先,我们将确定空间中值。 然后,我们将计算在影响病例中,与未受污染的泵相比,到布罗德街泵的相对距离有多重要。
我们将使用未加权的数据和根据该地点的案例数量加权的数据进行大部分分析,并使用不同的空间度量。 很有可能,按病例加权能更准确地描绘病例热点。 然而,它不太可能检测到一个很少发生的现象。 虽然未经加权的数据可以检测到这样的现象,但它很容易被异常值扭曲。
我们可以计算数据的空间中位数,并按该地点的个案数目加权:

当我们对数据进行加权时,空间中值将与病例的位置更加相关。这是因为病例很少的地区不会对数据产生太大的影响,而病例热点区将提供更大的影响。
当数据未加权时,空间中值与数据的范围和位置更相关,因为在边缘只有一个病例的位置与在中心有20个病例的位置具有相同的影响力。
空间中值位置使到每个病例位置的距离最小化。 因此,如果这些病例主要是由单一来源引起的,那么来源很可能是在空间中位数附近。 这使得确定一个区域以便更仔细地检查可能的来源非常有用。 注意:除非另有说明,默认的距离函数是EuclideanDistance(或地理空间数据的GeoDistance)。
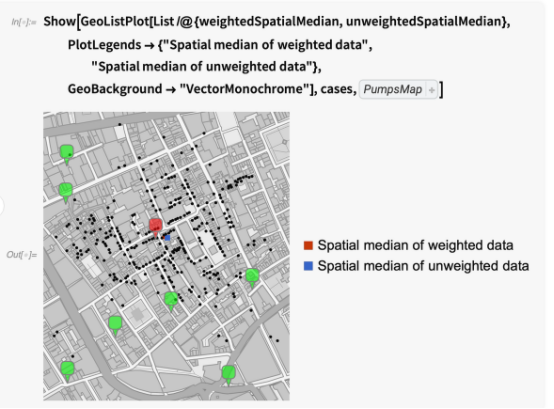
找到未加权的空间中值:

绘制空间中位数与病例的位置(使用 EuclideanDistance):
让我们使用不同的距离函数来计算空间中值:

根据泵的位置和病例,使用不同的距离函数绘制未加权空间中值的位置(注:一些空间中值位置重叠):
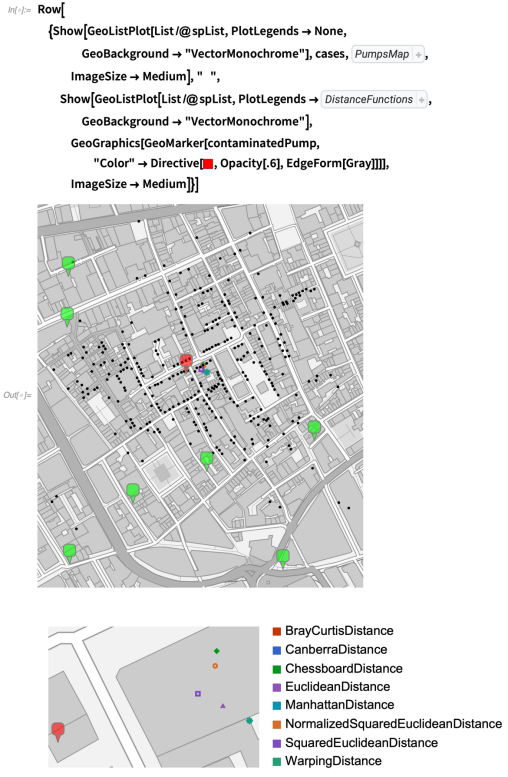
空间中值,无论是加权的、未加权的或具有不同距离函数的,都在布罗德街泵和其他泵的位置附近(见前面的可视化)。 这告诉我们,在一个位置的情况的数量是围绕空间中值近似旋转对称的。 否则,未加权的空间中值将与空间中值大不相同。
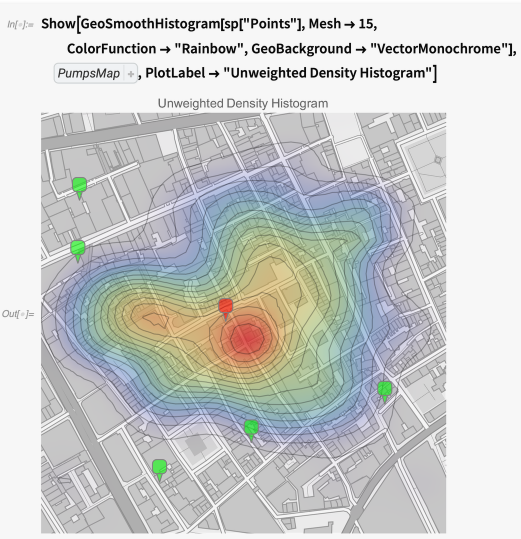
此外,查看下面的可视化显示,更多病例位置似乎更靠近数据中心。 这提供了一些轶事证据,说明只有一个数据源。
在该位置显示一个平滑的密度直方图的数据加权的病例数量:
显示病例位置的平滑密度直方图,忽略病例数:
接下来,我们将计算在布罗德街泵附近而不是另一个泵附近对某个地点的病例数量有多大影响。 这可能为布罗德街泵的责任提供了额外的证据。
我们计算一个度量,这仅仅是距离未污染泵与距离污染泵之间的比率。 我们预计,随着病例数量的增加,至少在某一点上,该比率的值也应该增加,因为当某一点更接近布罗德街泵时,该比率将增加:

我们可以创建一个病例和比率的BoxWhiskerChart,看看它是否显示了类似的现象,或者它是否是这种可视化方法的独特之处。
显示每个病例数量的比率的box-whisker图:
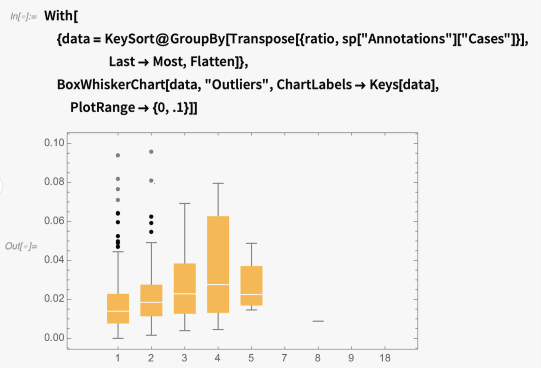
病例和比率似乎一起上升,直到5个病例,虽然中位数的上升仍然是线性的,但第75个百分位数似乎呈指数增长,这很有趣。 此外,当出现5例时,最低值和第25百分位继续上升。 这表明,我们之前的假设,低值可能是潜在的异常值,可能是正确的。 然而,我们仍然没有证据证明这一点,很可能有一些次要因素影响病例数量。
接下来,我们将测试比率和病例是否相互独立:

缺乏独立性提供了另一个证据,表明这个比率,以及到布罗德街泵和其他泵的距离,与病例有关。 在所有这些可视化和数据分析之间,我们可以说布罗德街的泵似乎更有可能与霍乱爆发有关,而其他泵对霍乱爆发的影响明显较小。
斯诺的地图说服了圣詹姆斯教区的守卫委员会,也就是水泵掉落的教区,把水泵的把手取了下来。 虽然对这种策略的整体有效性仍然存在疑问,因为霍乱爆发已经在下降,但斯诺发现的疾病传播的影响远远超出了1854年霍乱爆发。
事实上,斯诺可以被认为是“流行病学之父”,因为正如美国疾病控制和预防中心(CDC)在其网站上所说的那样,“他的工作阐明了从描述性流行病学到假设生成到假设检验(分析流行病学)到应用....的经典顺序”。
今天,如果您参观令人讨厌的布罗德街水泵所在的地方,您会发现对斯诺作品的双重纪念:一个水泵和他自己的“酒吧”——约翰·斯诺酒吧(这要感谢谷歌街景)。

致谢
我们要感谢Gosia Konwerska (Wolfram Research)提供的数据并帮助改进文章,感谢Jon McLoone (Wolfram Research)帮助将数据转化为实际地理位置,并提供了关于John Snow对流行病学贡献的历史和当代背景。
使用Mathematica 12.3或Wolfram|获得对最新的Wolfram语言功能的完全访问。