Wolfram：奇异欧拉-麦克劳林展开式 百年问题的新转折

 

关于和与积分

在所有数学运算中，加法是最基本的：这是我们在学校首先学到的。从历史上看，它是最古老的。虽然求两个数之和的任务很简单，但如果被加数的数量非常大，许多数之和很容易变成一个具有挑战性的数值问题。

 

大的总和在自然界中经常出现。例如，考虑一个由阿伏伽德罗数 N ≈ 10²³ 数量级的原子组成的固体。如果我们想要计算长程力，例如由于带电粒子之间的库仑相互作用，我们将不得不计算超过 10²³ 个被加数的总和，这在数值上是不可行的。

 

我们如何有效地计算大的（甚至无限的）总和？第一次尝试是通过积分来近似求和：

 

 

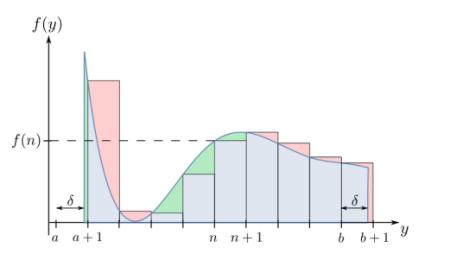
函数f（矩形）值的总和近似为积分（蓝色曲线）。但是我们看到在几何的某些部分，积分高估（绿色部分）或低估（红色部分）总和。但是这个积分近似有多精确？它可靠吗？我们可以改进它吗？

 

大约三百年前，著名数学家莱昂哈德·欧拉( Leonhard Euler)和科林·麦克劳林( Colin Maclaurin)首次尝试回答这个基本数学问题。他们独立发现了欧拉-麦克劳林求和公式（Euler-Maclaurin summation formula），该公式将总和与相关积分联系起来，这是一个非常重要的结果，至今仍在数值实践中使用，并在Mathematica的Nsum例程中作为EulerMaclaurin方法实现。公式如下：

 

 

 

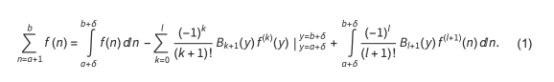
这个和用一个任意偏移δ∈(0,1)的积分来近似求得。积分逼近的高阶修正用求和函数在积分边界处的导数来描述。这些导数的系数是由周期伯努利函数Bk构成的。

 

在Mathematica中，与周期伯努利函数(0,1)重合的伯努利多项式被实现为BernoulliB。我们周期性地将这些函数扩展到实线，注意到l = 1的函数在整数处是不连续的(参数1+y - ceiling [y]的选择使其左侧极限始终存在):         

 

 

 

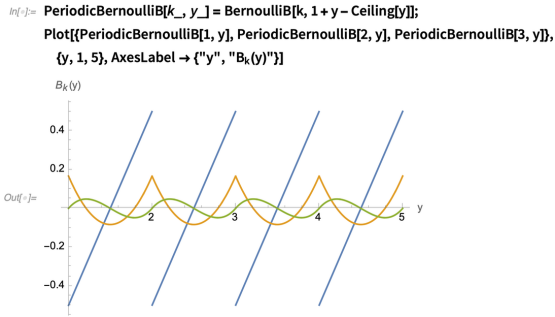
求和公式的收敛性由伯努利周期函数B k随着k → ∞的渐近行为决定。我们可以通过创建周期性伯努利函数的最大绝对值表来快速分析这种行为：

 

 

 

上图显示了众所周知的估计

 

 

 

这意味着欧拉-麦克劳林展开式收敛的重要条件，即

 

 

 

σ < 2 π。这对应于在傅立叶空间中具有足够小的带宽的带限函数f。如果函数f包含一个代数奇点，例如f ( y ) = | 是| -v，然而，导数规模为

 

 

 

并且扩展的其余部分发散为k → ∞。

 

我们可以使用 Mathematica 的Asymptotic函数验证奇异相互作用的渐近尺度：

 

 

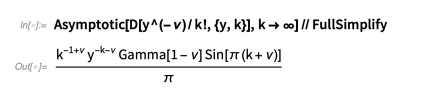
因此，如果被加函数包括奇点，则扩展的用途有限。您可能会问，“我们为什么要关心奇异函数？这些功能是否具有足够高的实际相关性，以至于我们应该担心它们？” 事实证明，它们具有足够高的实际相关性。

 

基本力的小故事

据我们所知，物理学中有四种基本力。在这四种中，有两种是长程的，即电磁相互作用和引力相互作用。（我们暂时不会考虑弱相互作用和强相互作用，因为它们只作用于核尺度。）这些力不仅随距离缓慢衰减，而且还是奇异的。由距离-y尺度分隔的两个粒子的引力相互作用和静电能V为

 

 

 

并且各自的力F遵循平方反比定律：

 

 

 

因此，如果两个粒子无限接近，势能和合力都会发散。从这些基本的相互作用中，可以产生更一般的相互作用，例如

 

 

 

例如，其中v = 3 描述了磁性粒子之间的偶极相互作用。

 

在自然界中，我们很少处理少量的粒子（原子或分子）。在大多数情况下，例如在凝聚态系统中，手头的系统是由非常非常多的粒子形成的。粒子之间的相互作用创造了整体固体的特性。然而，如果我们想计算固体中的力，我们必须评估这种类型的总和（例如在 1D 中）

 

 

 

其中u描述了粒子从具有相等最近邻距离的晶体的位移。如果粒子数N很大，计算这个总和是一项非常艰巨的任务，即使位移函数u是已知的。现在很自然地尝试通过积分来近似求出这个复杂的力和，并通过欧拉-麦克劳林展开式写出有限大小的修正。然而不幸的是，F是奇异的，因此欧拉-麦克劳林求和中的误差项发散。这最终会导致不受控制的错误，并且通常会导致错误的近似。欧拉-麦克劳林展开法是一种已有三百年历史的可靠的大型数值分析工具，在试图处理出现在现代物理学中的总和时，它达到了极限。我们需要的是一个新的扩展，能够在在旧扩展失败之处通过考验。

 

奇异欧拉-麦克劳林展开式

 

我们现在改进了原始的欧拉-麦克劳林展开式，使其适用于出现在凝聚态物理中的奇异函数。但是，如何补救看似不可避免的扩张分歧呢？我们考虑以下形式的函数f

 

 

 

其中 s(y) = | y |–v，x = ∈ ?。我们称s为交互作用，g为插值函数。正如我们之前看到的，余数项的发散是由于取相互作用的导数而产生的。我们接下来的策略是避免这些导数，取而代之的是采用函数g 的导数。相互作用包含在这些导数的系数中。这些系数是由周期性伯努利函数的泛化形成的，我们称之为伯努利-A 函数。

 

我们使用Mathematica对Hurwitz zeta函数的高效实现，实现了ref.[1]的eq.(12)中给出的伯努利-A函数:  

 

 

 

对于z∈?，伯努利- a函数在极限v→z中仍然有很好的定义:

 

 

 

奇异欧拉-麦克劳林(SEM)展开式如下:  

 

 

 

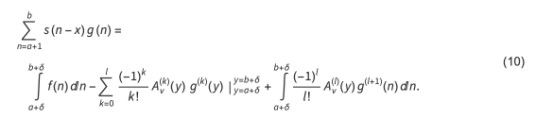
如果函数g有足够的带限，那么这个扩展的误差——如果我们丢弃余数积分——在扩展顺序中呈指数下降。因此，我们设法创建了一个新版本的欧拉-麦克劳林展开式，它可以应用于具有奇点的函数。

 

让我们看第一个例子。

 

应用的第一步：Euler-Mascheroni 常数

奇异欧拉-麦克劳林展开式的第一个简单应用是计算著名的Euler-Mascheroni 常数γ，它在 Mathematica 中作为EulerGamma 实现。人们对这个难以捉摸的数量知之甚少。例如，γ 是否是无理数是数学中的一个悬而未决的问题：

 

 

 

它的值是一个和与一个积分之间的差的极限：

 

 

然后我们可以将 SEM 扩展应用于和与积分之间的差异，它仅由零阶贡献组成：

 

 

 

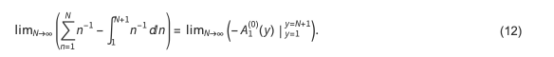
y = N + 1处的评估在N → ∞极限处消失，y = 1处的值产生所需的结果：

 

 

 

让我们认真起来：畴壁中的远程力

为了演示膨胀的性能，我们将其应用于具有长程相互作用的一维晶体内部力的计算：

 

 

 

在前面的插图中，我们看到晶体中有一种特殊的密度调制，称为畴壁。这个宽度为 λ 的畴壁将粒子从它们的平衡位置（虚线圆圈）移开。它构成了具有晶体有序性的区域之间的边界，其中粒子具有相等的距离。

 

为什么畴壁与现代科学相关？好吧，畴壁出现在分层材料中。畴壁是晶体结构中的缺陷，在新材料的设计中非常重要，因为它们的存在可以改变底层材料的特性，例如其弹性或电特性。我们现在的目标是计算周围所有粒子对红色粒子施加的力。如果晶体由大量粒子组成，则力计算带来了极具挑战性的数值问题。

 

在我们处理数值任务之前，我们首先需要指定畴壁的轮廓，它描述了粒子从等距网格的位移。 我们将选择一个位移函数插值在0和1之间的畴壁，它对应于链中的离域粒子孔。

 

畴壁的位移函数以 0 为中心，通过对宽度为 λ 的归一化洛伦兹积分从负无穷大到y 来实现，从而获得在 0 (–∞) 和 1 (+∞) 之间插值的函数：

 

 

 

 

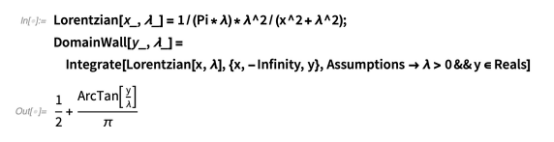
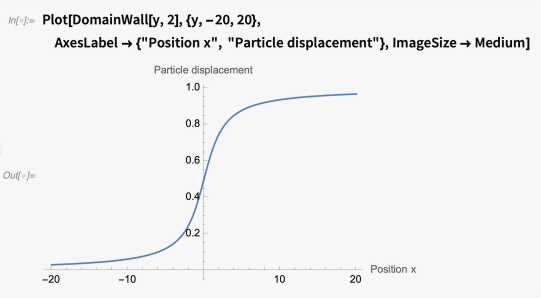
然后我们计算力总和：

 

 

 

去除物理尺寸后，我们发现

 

 

 

和

 

 

 

我们现在的策略是将被加函数分解为奇异因子s和平滑函数因子g

 

 

 

和

 

 

 

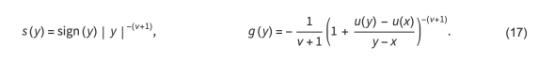
我们假设位移足够小，使得粒子保持有序（因此g中括号中的项始终为正，不需要绝对值）。下面，我们考虑带电粒子之间的库仑力 ( v = 1)。请注意，我们没有应用任何力的线性化，因为我们的方法也完全适用于非线性函数g。

 

我们定义了交互作用s的函数、插值函数g和相应的函数f。一个小的数值偏移被添加到v 0的值中以简化实现：

 

 

 

我们随后指定晶体和畴壁的大小。在第一种情况下，我们选择了 2,000 个粒子的微观晶体和 10 个原子距离的畴壁宽度。在第二个例子中，我们将探讨如果晶体的宏观尺寸为 2 × 10¹⁰粒子，畴壁宽度为 λ = 10⁵，会发生什么情况：

 

 

 

在物理学界，力和通常简单地用积分代替。现在让我们研究在这两种情况下，这个积分近似如何准确地再现力。  

 

我们首先为各自的力生成表格。

 

积分近似与宣泄的危机

下图比较了通过精确求和获得的力与积分近似值。

 

我们显示了精确的力（蓝点）和使用细观链的积分近似（橙色线）计算的力：

 

 

 

 

精确求和与积分近似值都显示了粒子被拉向畴壁的定性行为。这是有道理的，因为畴壁是一个离域粒子孔，其他粒子倾向于重新填充。然而，从上图中可以清楚地看出，积分方法严重低估了力的绝对值。因此，它只能用于定性，而不能用于任何类型的定量预测。小的修正会对材料特性产生相当大的影响。为了精确预测，需要比积分近似更好的方法。我们现在证明使用我们的 SEM 扩展可以大大提高积分的精度。

 

从积分近似到 SEM 实际上非常简单。我们只需要实现局部SEM微分算子

 

 

 

并且必须在集成的边界处对其进行适当的评估。

 

我们使用我们之前展示的伯努利-A 实现和 Mathematica 的自动微分功能来定义 SEM 算子：

 

 

 

我们使用积分偏移δ0 = 1的一阶SEM展开。

 

设置膨胀参数并定义力总和的 SEM 近似值：

 

 

 

我们再次计算力的近似值，但现在进行了额外的 SEM 校正。

 

我们使用域壁宽度的适当重新缩放来计算力总和的 SEM 近似值。ParallelTable允许并行执行计算：

 

 

 

最后，我们将精确力（蓝点）与积分近似（橙线）和 SEM 扩展（红线）进行比较：

 

 

 

仅使用一阶 SEM，这相当于仅计算g的单个导数，我们达到的精度使 SEM 近似值与精确结果在视觉上无法区分。请记住，校正是局部性质的，可以很容易地计算出来。因此，我们现在可以计算更大的粒子数，而通过求和来计算精确的力是不可能的。

 

宏观任务

我们现在转到宏观系统，计算由 2 × 10¹⁰ 粒子和宽度为 λ = 10⁵的畴壁组成的晶体中的力。

 

显示了从 SEM 扩展（蓝线）和积分近似（橙线）计算的宏观晶体中的力：

 

 

 

在这里，积分近似（橙色）和 SEM 扩展（蓝色）都保持可计算，因为两者都表现出不依赖于系统大小N的运行时间。然而，对精确总和的评估在数值上变得不可行。我们看到，即使N是宏观的（在 10 ^–10 m的典型粒子间距离处，晶体将有两米长），积分近似和 SEM 扩展之间仍然存在显著差异。在这里，我们看到了一个非常有趣的效果，即具有库仑相互作用的一维系统中的有限尺寸校正在所有尺度上都保持相关并且永远不会被真正忽视。

 

总结

自从欧拉和麦克劳林提出求和公式的第一个版本以来，已经过去了几个世纪。我们现代版本的扩展实现了对现代科学产生影响的这一承诺：解决关于如何在从离散到连续的过程中正确处理奇点的开放性问题。